Scroll
near
the text to view everything. (This example is a long one)Chain Rule
Below is the formula to chain rule: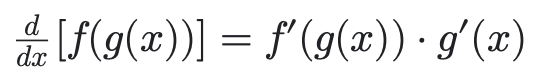
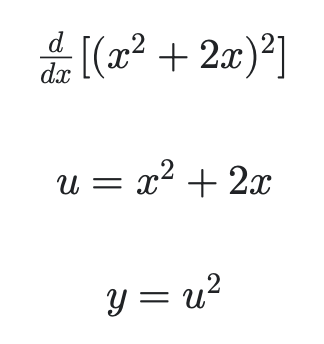 As you can see we are sepearting the function into simpler terms of y and u. In this case g(x), or u, is (2x cubed + 2x), and y is u squared (remember we are subsituting u for g(x)). We'll then take the derivative of both y and u.
As you can see we are sepearting the function into simpler terms of y and u. In this case g(x), or u, is (2x cubed + 2x), and y is u squared (remember we are subsituting u for g(x)). We'll then take the derivative of both y and u.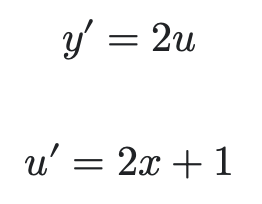 After taking the derivative, like mentioned in the formula, we'll multiply the two. Remember that f'(g(x)) is u' and g'(x) is y'.
After taking the derivative, like mentioned in the formula, we'll multiply the two. Remember that f'(g(x)) is u' and g'(x) is y'.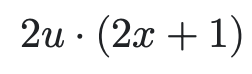 But remember, in our final equation we can't have the answer in terms of u, so instead we'll subsitute u for what we defined earlier, which was x square + 2x, and all we have to do then is simplify.
But remember, in our final equation we can't have the answer in terms of u, so instead we'll subsitute u for what we defined earlier, which was x square + 2x, and all we have to do then is simplify.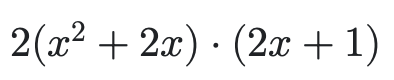
Go BackIf you look closely we are basically taking the derivative of a composite function. Now there's a simpler method to applying the chain rule, which is to imagine g(x) as u. This is method is easier to understand through solving an example like the one shown below.
For example,